Empower education with smart automation.

Track student progress, organize content effortlessly, and amplify learning impact for everyone. Let intelligent automation enhance education—supporting students, teachers, and parents with smart insights. In the digital era, education becomes even more powerful.

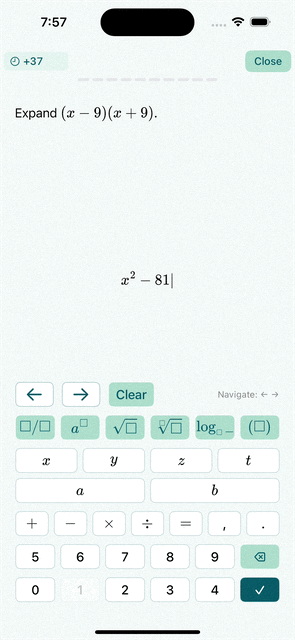
Complete Example: 2(3x−5)−4(2x−3)2(3x-5)-4(2x-3)

See how our three-stage approach transforms complex algebraic problems into manageable learning.

Stage 1: Definition Mastery

Students first learn what each multiplication means in plain language.

2(3x−5)2(3x-5)
= "Add (3x-5) itself twice"
4(2x−3)4(2x-3)
= "Add (2x-3) four times"

Stage 2: Logical Development

Using their definition knowledge, students work through the logical steps systematically.

2(3x−5)=(3x−5)+(3x−5)=3x+3x−5−5=6x−102(3x-5) = (3x-5)+(3x-5) = 3x+3x-5-5 = 6x-10
4(2x−3)=(2x−3)+(2x−3)+(2x−3)+(2x−3)=8x−124(2x-3) = (2x-3)+(2x-3)+(2x-3)+(2x-3) = 8x-12
2(3x−5)−4(2x−3)=(6x−10)−(8x−12)2(3x-5)-4(2x-3) = (6x-10)-(8x-12)
=6x−10−8x+12= 6x-10-8x+12
=6x−8x−10+12= 6x-8x-10+12
=−2x+2= -2x+2

Stage 3: Fluency Training

After mastering stages 1 and 2, students practice until they can solve complex problems mentally in one step.

2(3x−5)−4(2x−3)2(3x-5)-4(2x-3)
↓
2×3−4×2=−22\times3-4\times2=-2
2×(−5)−4×(−3)=22\times(-5)-4\times(-3)=2
↓
−2x+2-2x+2
Goal: One-step mental calculation of complex expressions

This fluency training is achieved through our interactive Trainer app, which provides personalized practice sessions.

Learn about Trainer App →

Real Problems, Real Solutions

See how SeedTree identifies and fixes common student errors

a+b≠a+b\sqrt{a} + \sqrt{b} \neq \sqrt{a + b} Proof

By squaring both numbers, students should be able to prove why a+b\sqrt{a} + \sqrt{b} is not equal to a+b\sqrt{a + b}

📝Example Question

Prove that 2+3\sqrt{2} + \sqrt{3} is not equal to 5\sqrt{5}
❌
Current Approach

Most students get confused with this after memorizing:

a×b=ab\sqrt{a} \times \sqrt{b} = \sqrt{ab}

They incorrectly apply multiplication rules to addition

✅
Improved Approach

SeedTree guides students to:

The Coefficient of x: 1. Square (2+3)2(\sqrt{2} + \sqrt{3})^2
The Constant: 2. Expand to 2+26+32 + 2\sqrt{6} + 3
3. Compare with (5)2=5(\sqrt{5})^2 = 5
∴ They are not equal

12x3=2x−3\frac{1}{2x^3} = 2x^{-3}

Only the index form moves to the numerator, not the entire denominator including multiplier

❌
Common Mistake
12x3=2x−3\frac{1}{2x^3} = 2x^{-3}

Incorrectly moving entire denominator

✅
Correct Method
12x3=12×1x3=12x−3\frac{1}{2x^3} = \frac{1}{2}\times\frac{1}{x^3}= \frac{1}{2}x^{-3}

Only the index form moves up

Why this matters: Understanding the rules of exponents is crucial for algebra and calculus. SeedTree helps students see why rules work, not just memorize them.

Build deep mathematical understanding step-by-step.

Our three-stage approach: master definitions, develop logical reasoning, then build computational fluency.

Trainer

Interactive platform where students practice fluency training through personalized sessions to achieve one-step mental calculation of complex expressions.

Worknote

Structured practice platform for building computational fluency after conceptual mastery is achieved.