For Teachers
Master our three-stage methodology: definition mastery, logical reasoning, and computational fluency for truly effective mathematics education.
Our Teaching Mission
We believe every student can master mathematics through deep understanding, not just memorization. Our systematic three-stage approach helps teachers build genuine mathematical thinking that lasts a lifetime.
Build Mathematical Understanding Step-by-Step
SeedTree provides teachers with a systematic three-stage methodology that builds genuine understanding. Instead of teaching shortcuts, we help students master mathematical definitions, develop logical reasoning, and then build computational fluency.
Three-Stage Methodology
Systematic approach from definition mastery through logical development to fluency training.
Deep Conceptual Learning
Students build genuine understanding that lasts, not temporary memorization of procedures.
Long-Term Results
Students carry deep understanding into advanced mathematics, not just procedural memory.
Teaching Philosophy in Action
Start with Definitions
Before any calculation, ensure students understand what operations mean. 2(3x-5) isn't just a formula—it's "Add (3x-5) twice."
Develop Logic Step-by-Step
Guide students to translate definitions into logical steps. Show them how (3x-5)+(3x-5) naturally becomes 6x-10 through reasoning.
Train for Fluency
Only after mastery of stages 1 and 2, practice for speed. The goal: 2(3x-5)-4(2x-3) → -2x+2 becomes automatic.
Track Student Learning with Improvement Points
Identify and address common mathematical misconceptions with our improvement point system. Record frequent student mistakes and track which students need targeted support for specific concepts.
Why Improvement Points Matter
Common Student Misconceptions
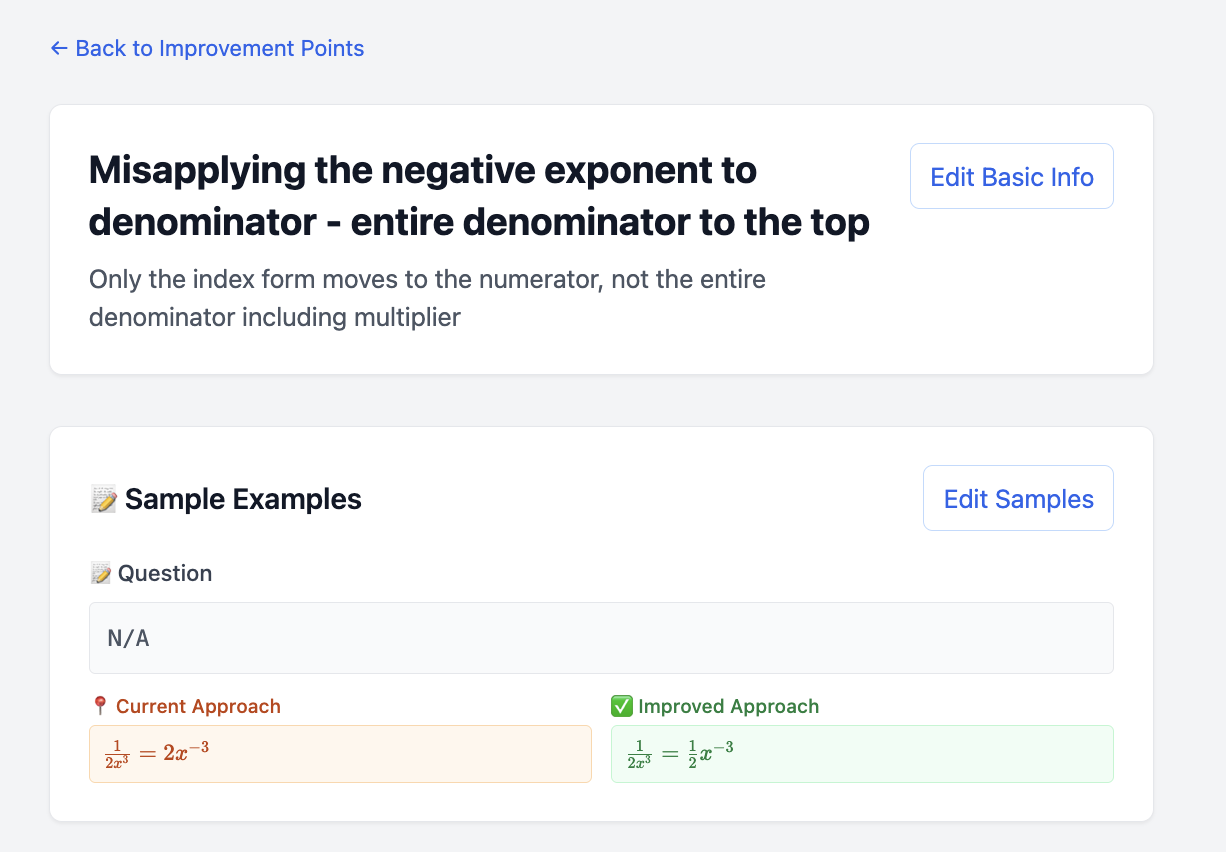
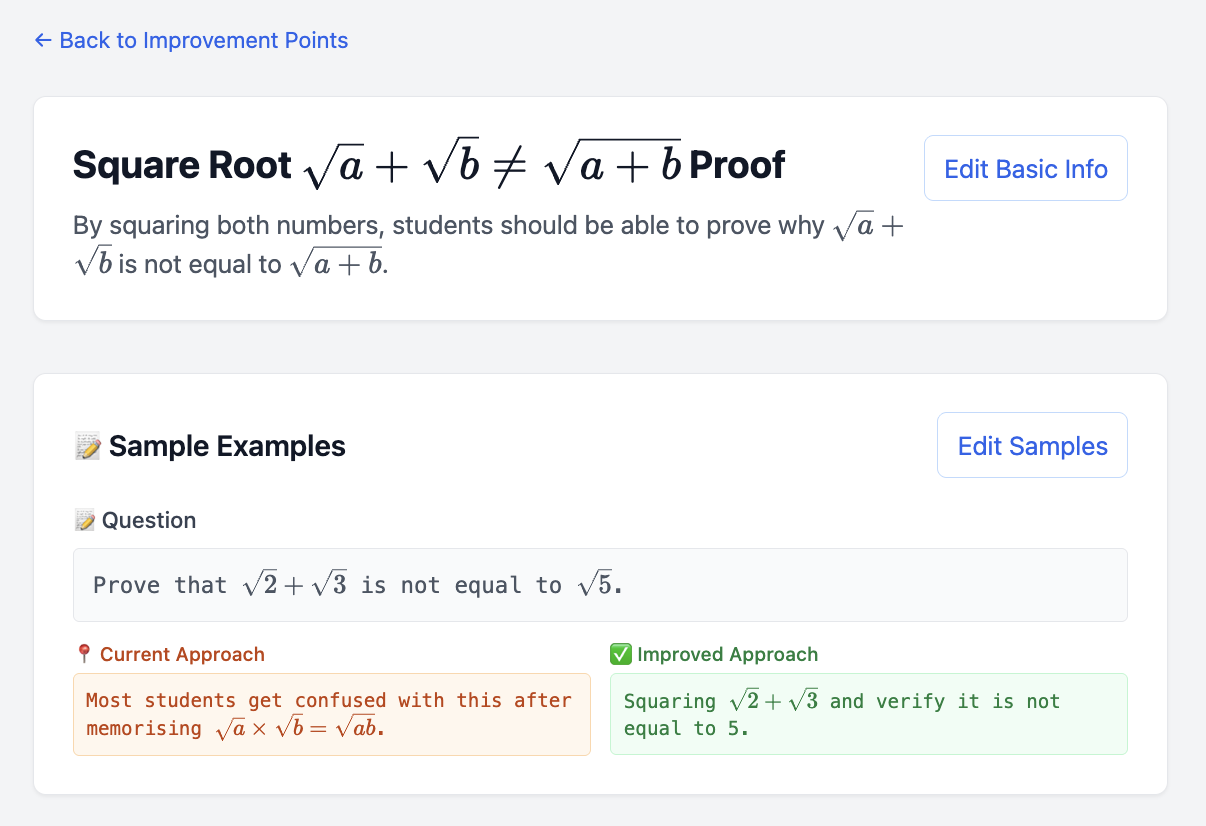
Mathematics education is full of predictable mistakes. Students often confuse √a + √b with √(a + b), or apply distributive properties incorrectly. Our improvement points help you catalog these common errors systematically.
Personalized Student Tracking
Assign improvement points to individual students to track their specific learning needs. See exactly which students struggle with which concepts, enabling targeted intervention and personalized support.
Data-Driven Teaching Decisions
Use concrete data about student misconceptions to guide your lesson planning. Focus class time on the areas where students most need support, making your teaching more efficient and effective.
Improvement Points in Action
Example: Square root misconception improvement point
Example: Negative exponent misconception improvement point
How Improvement Points Transform Your Classroom
1. Identify Patterns
Catalog the most common mistakes students make across different mathematical concepts
2. Assign to Students
Track which specific students struggle with which concepts for personalized learning support
3. Target Intervention
Use data-driven insights to focus your teaching on areas where students need the most help
Complete Teaching Example: 2(3x-5)-4(2x-3)
Stage 1: Definition Teaching
Help students understand:
Stage 2: Logical Reasoning
Stage 3: Fluency Training
Train students for mental calculation:
How to Implement the Three-Stage Approach
Stage 1: Definition Mastery
Begin every new concept by ensuring students understand the fundamental definition. Don't rush to procedures—build the conceptual foundation first.
Ask: "What does multiplication mean?"
Teach: 2(3x-5) = "Add (3x-5) to itself twice"
Check: Have students explain 4(2x-3) in their own words
Stage 2: Logical Development
Guide students to use their definition knowledge to work through problems logically. Emphasize understanding over speed at this stage.
Stage 3: Fluency Training
Only after stages 1 and 2 are mastered, practice for computational speed. The goal is mental calculation of complex expressions.
Teacher Benefits
Clear Teaching Framework
No more guessing how to teach complex concepts. Our three-stage approach gives you a proven, systematic method for every algebraic topic.
Student Success
Watch your students develop genuine confidence as they understand WHY mathematics works, not just HOW to get answers.
Reduced Preparation Time
Our structured approach means less time planning lessons and more time focusing on student understanding and engagement.
Advanced Teaching Strategies
Definition Mastery Techniques
Begin every new concept by ensuring students understand the fundamental definition. Don't rush to procedures—build the conceptual foundation first.
Teaching Sequence:
Ask: "What does multiplication mean?"
Teach: 2(3x-5) = "Add (3x-5) to itself twice"
Check: Have students explain 4(2x-3) in their own words
Practice: Multiple examples until definition is automatic
Logical Development Framework
Guide students to use their definition knowledge to work through problems logically. Emphasize understanding over speed at this stage.
Step-by-Step Logic:
Fluency Training Methods
Only after stages 1 and 2 are mastered, practice for computational speed. The goal is mental calculation of complex expressions.
Fluency Goal:
Ready to Transform Your Teaching?
Join educators worldwide who are building mathematical understanding the right way.